Expand UserActionAttachment & PoliticalActionAttachment To All Resources
-
The "userActionAttachment" could really use another method of payment for each action in addition to PUs.
I suggest expanding the existing code for below to be able to use a resource .
Existing: "costPU" value: Amount of PU you will be charged to attempt this action.
Suggested: "costResource" value: Amount of resource you will be charged to attempt this action.
I am currently trying to get my new technology model to function via "userActionAttachments" for "Big World 3 : Final Solution". I would love to use a resource like "political capital" or "political influence" in addition to some PUs. This would give me a nice mechanism of purchasing and activating technologies, that does not involve any randomness at all.
Nations would receive some free "political influence" each turn depending on their governments ideoIogy. For instance a democratic government means it's harder to get things done if you have a healthy opposition, so you get less free "political influence" as leader of USA or UK. A fascist ideology as in Germany or Italy would have more "political influence" to get things done since there is virtually no political opposition. Also I intend to make objectives that each nation needs to accomplish in order to obtain additional "political Influence" that is needed to push through a initiative, such as developing a new technology. Also I would like to offset "political influence" with traditional resources.
I could use resources like iron, oil, and rubber to develop the technologies as well. This would give the nations additional reasons to go for certain territories and regions. Which will promotes variety and less scripted moves.
XML
<attachment name="userActionAttachment_6_Finland_receives_financial_support" attachTo="Germany" javaClass="games.strategy.triplea.attachments.UserActionAttachment" type="player"> <option name="conditions" value="conditionAttachment_Finland_receives_financial_support"/> <option name="activateTrigger" value="triggerAttachment_Finland_receives_financial_support-1:1:false:false:false:false"/> <option name="activateTrigger" value="triggerAttachment_Finland_receives_financial_support-2:1:false:false:false:false"/> <option name="text" value="Germany_Finland_10_PUs"/> <option name="costResources" value="10:PUs"/> <option name="costResources" value="2:Iron"/> <option name="costResources" value="1:Fuel"/> <option name="attemptsPerTurn" value="1"/> </attachment>Result
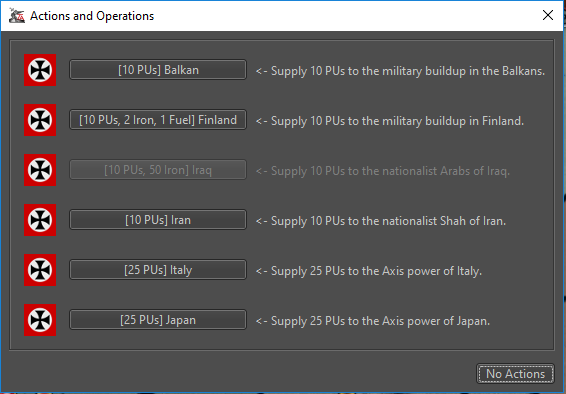
-
@general_zod Yeah, out of all your blue sky suggestions (I do like them!) this is the only one that has a chance of being implemented. There is just simply no reason why you should restrict user action cost to PUs; it doesn't even really make the code simpler or anything.
I would suggest a different xml implementation though, which is "cost" value="10:PUs:10:oil:5:iron:1:PoliticalInfluence".
-
I was hoping that if implemented, that it was possible to enter the cost on multiple lines for a single user action. However I like your idea better. It assures cost can be split between PUs and multiple resources, for a single user action.
-
@general_zod This is actually captured already here in #3: https://forums.triplea-game.org/topic/128/resource-system-assessment-and-improvements
-
I knew I saw related post somewhere.
I love the idea to be able to check any resource via conditions. It will open up some creative ideas.
As they relate to user actions, will the conditions be rechecked continuously?
Lets say I have 3 user actions and each one has a mixture of 5 different resources, something like so.
-
"Jet Power" - cost = 5 political influence, 30 PUs, 10 Aluminum, 5 Steel, 10 oil.
-
"Improved Artillery" - cost = 5 political influence, 30 PUs, 5 Aluminum, 20 Steel, 10 oil.
-
"Submarine Advances" - cost = 10 political influence, 30 PUs, 5 Aluminum 20 Steel, 20 oil.
Lets say " jet power" is chosen, this will activate a trigger to subtract the required resources and activate technology. Will the condition that checks for adequate resources, be rechecked after the initial expenditure is made? So further actions can be paid for without issues, all on the same sequence step?
-
-
I'm aware I that I can use the production phase to do essentially the same thing. However, currently there is no way to prevent the additional non combat units needed from cluttering the "unit help" feature. This side effect renders the "unit help" to cumbersome to be as useful as first intended. Especially for the noobies, it becomes a source of confusion instead.
So here is another suggestion for feature.
An attribute which can set, if this unit will be displayed in "unit help". Maybe in the "unitAttachment" as so.
<attachment name="unitAttachment" attachTo="Jet-Power" javaClass="games.strategy.triplea.attachments.UnitAttachment" type="unitType"> <option name="unitHelp" value="false"/> </attachment> -
So I'm revisiting this feature request since this has now come up across a few different maps. Initial plan is to add cost resources besides PUs to user and political actions. I'm open to suggestions on XML format and option name but my initial thought is to make it similar to unit option "createsResourcesList":
<attachment name="userActionAttachment_Americans_Aid_UK" attachTo="Americans" javaClass="games.strategy.triplea.attachments.UserActionAttachment" type="player"> <option name="costResources" value="3:PUs"/> <option name="costResources" value="2:steel"/> </attachment>Could go with just "cost" instead of "costResources" and could consider doing it on 1 line like @alkexr mentioned instead of separate option lines for each resource. But my initial thought is try to keep it somewhat consistent with "createsResourcesList" unless convinced otherwise.
-
@redrum As I said in the other thread, I think having an option for testing the presence of the resources (to remove) and a different option for removing resources ("createsResourcesList" with negative values, that is already there) seems better to me, and in line with how everything else works (you don't have a single option for testing relationships and changing them, etc.), instead of a single option that both tests presence and remove the resources, but it seems that not everyone is getting it, not sure why; so I guess this version (a single option both testing you have X resources and removing them) has the benefit of being easier to understand for most, looks like.
By the way, a thing I didn't specify is that my suggested way, if meant to work for politics too, not only for user action, needs either the addition of the "activateTrigger" support to them too, or a direct support of the "createsResourcesList" in the action, that I would anyway advice (as currently you can give/remove resources with user actions, via the aforementioned trigger option, but not with political actions).
Side note, while at it, I suggest having a way to specify to remove all in "createsResourcesList", so we don't have to set it at -10000 or something (already a few maps going this way).
-
@cernel said in Resource System Assessment and Improvements:
To make a clear example, now you can give 4 PUs from Americans to British by:
- Having a costPU=4
- Having a trigger adding 4 PUs to British
If you would be able to test for resources you could do it by:
- Having a condition for testing Americans having 4+ PUs
- Having a trigger removing 4 PUs from Americans
- Having a trigger adding 4 PUs to British
All the triggers are already there; it is just needed the condition for testing the presence of any resources, comprising PUs. So, I would go this way, instead of extending the costPU, as this being much more extensive.
An example may be that you want the Americans being unable to give all their income to the British, and you could do this by giving X and testing Y, where Y may be equal to 2X (the Americans are limited giving at most half their income to the British). Of course, you could use the ability to test for resources for totally different reasons, as well.
Anyways, I've said this a bunch of times and, as much at it seems obvious to me, it seems to confuse others, so I guess just expanding the costPU is what most are actually requesting.
-
@cernel While I get what you are saying, I think the majority of folks and convenience of a simple option for user/political actions that does both overruled you. Adding resource check for conditions is still something that would be nice to add but is lower priority as its been much less requested than this.
-
@redrum I think most don't think about it at all, but just look at the costPU and think about expanding it to any resources, so I think most are just not getting what I'm saying (not realising that testing resources would fully cover) or overlooking it. Anyways, it is true I don't appear to have convinced anyone, as I already pointed out myself.
One way or the other, being able to actually use resources is a big step ahead (tho you can currently do it by hacking units into simulating resources in boxes or whatever), just to clarify I'm supportive. -
Here is the PR: https://github.com/triplea-game/triplea/pull/3459
XML
<attachment name="userActionAttachment_6_Finland_receives_financial_support" attachTo="Germany" javaClass="games.strategy.triplea.attachments.UserActionAttachment" type="player"> <option name="conditions" value="conditionAttachment_Finland_receives_financial_support"/> <option name="activateTrigger" value="triggerAttachment_Finland_receives_financial_support-1:1:false:false:false:false"/> <option name="activateTrigger" value="triggerAttachment_Finland_receives_financial_support-2:1:false:false:false:false"/> <option name="text" value="Germany_Finland_10_PUs"/> <option name="costResources" value="10:PUs"/> <option name="costResources" value="2:Iron"/> <option name="costResources" value="1:Fuel"/> <option name="attemptsPerTurn" value="1"/> </attachment>Result

-
@redrum I wouldn't have the display like "[10 PUs, 2 Iron, 1 Fuel]", or anything like that at all. The mapmaker can just add it in the customised description, exactly as it reads now, or differently, so I don't see the point of having any automated description, there, unless maybe only if the button is not customized at all.
Another difference, and something you may want to consider, is whether the cost resource is paid in any case or only if successful, in all or some cases.
For example, if Finland have to accept the aid and refuses, do you still pay the cost for nothing?
For example, you have an user action to hire a Ninja, with a chance to succeed: should you pay the cost in all cases or only if the action is successful?
For example, you have a political action to Ally a player at some cost for you, if he consents: should you pay the cost no matter if he refuses or only if he accepts?
Under my suggestion, the cost would have been paid only if the action was successful (as it would remove resources with a trigger that needs to be activated by the action).
The current behaviour (unless recent changes) is to always pay the cost, no matter if the action is successful.
I remember this felt dumb back when Napoleonic Empires FFA had costs to upgrade relationships, as you would pay that cost no matter if the other side refused, so you needed to chat to try to be assured the other guy was going to accept it, not to just waste money for nothing (but then Veqryn removed all action costs from that game, so it doesn't matter anymore for that one).
On this point, my suggestion is supporting both (the mapmaker being able to decide whether the cost is paid always or only for successful actions). -
@cernel I've noticed a problem with the check-then-remove approach while thinking about it. The conditions only check whether you had enough resources before the user actions phase. If you spend resources for user actions, the conditions won't be reevaluated, and all other user actions will still be available regardless of whether you have enough resources or not. At least this is my understanding of how conditions work.
-
@alkexr As I already said, conditions are tested upon getting the actions panel. Just test it.
-
@cernel You can test it with "Napoleonic Empires: FFA 5 Player", if you set Relationships Last Extra Rounds equal to -1.
Conditions are tested anew after each time you take an action, and this is intended. -
The ability to check any resource quantity for any players in conditions is a cool feature and has much potential. I would love to see it come to fruition someday. I'm not one to hold back progress but it should be a separate feature request.
There are overlapping functionality, but as it relates to user/political actions specifically, as I understand it, it will require more xml code to implement the same outcome as compared with this method. Also this assumes you are correct about the conditions being constantly checked and rechecked for multiple user/political actions performed on same players phase (after each individual action).
Anyways the 2 methods each have advantages and disadvantages but are not mutually exclusive. Meaning we can still hopefully get your method and all its functionality, down the road. This would also keep in line with existing xml structure as well, as there are currently areas where the same outcome can be achieved by different methods.
-
Cool feature. I look forward to implementing it in Big World 3 once it is merged. Thanks.
-
@cernel Can't really remove the auto display of the resources amounts as that would pretty much make any existing maps that use them unusable. Unless you are volunteering to find/update all of them

And if something has a chance to succeed then whether it does or doesn't I'd expect the player to pay for it. Similar to tech tokens.
-
@redrum Ok, but you probably mean similarly to v2 tech, then. Since v3 tech (token based) you keep the tokens if failing, that is effectually closer to paying the cost only with success (the only difference is that the tokens oblige you to try again, instead of using the money for something else).
I agree that would be good to update all maps having costPU, especially for, then, removing the costPU from the engine (instead of merely deprecating it), in favour of the new costResources. If @Frostion is good with that for his maps, I can look updating the rest. Agreed?